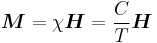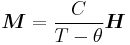Paramagnetism
Paramagnetism is a form of magnetism whereby the paramagnetic material is only attracted when in the presence of an externally applied magnetic field. In contrast with this, diamagnetic materials are repulsive when placed in a magnetic field. Paramagnetic materials have a relative magnetic permeability greater or equal to unity (i.e., a positive magnetic susceptibility) and hence are attracted to magnetic fields. The magnetic moment induced by the applied field is linear in the field strength and rather weak. It typically requires a sensitive analytical balance to detect the effect and modern measurements on paramagnetic materials are often conducted with a SQUID magnetometer.
Paramagnetic materials have a small, positive susceptibility to magnetic fields. These materials are slightly attracted by a magnetic field and the material does not retain the magnetic properties when the external field is removed. Paramagnetic properties are due to the presence of some unpaired electrons, and from the realignment of the electron paths caused by the external magnetic field. Paramagnetic materials include magnesium, molybdenum, lithium, and tantalum.
Unlike ferromagnets, paramagnets do not retain any magnetization in the absence of an externally applied magnetic field, because thermal motion randomizes the spin orientations. Some paramagnetic materials retain spin disorder at absolute zero, meaning they are paramagnetic in the ground state. Thus the total magnetization drops to zero when the applied field is removed. Even in the presence of the field there is only a small induced magnetization because only a small fraction of the spins will be oriented by the field. This fraction is proportional to the field strength and this explains the linear dependency. The attraction experienced by ferromagnetic materials is non-linear and much stronger, so that it is easily observed, for instance, by the attraction between a refrigerator magnet and the iron of the refrigerator itself.
Contents |
Relation to electron spins
Constituent atoms or molecules of paramagnetic materials have permanent magnetic moments (dipoles), even in the absence of an applied field. This generally occurs due to the spin of unpaired electrons in the atomic/molecular electron orbitals (see Magnetic moment). In pure paramagnetism, the dipoles do not interact with one another and are randomly oriented in the absence of an external field due to thermal agitation, resulting in zero net magnetic moment. When a magnetic field is applied, the dipoles will tend to align with the applied field, resulting in a net magnetic moment in the direction of the applied field. In the classical description, this alignment can be understood to occur due to a torque being provided on the magnetic moments by an applied field, which tries to align the dipoles parallel to the applied field. However, the true origins of the alignment can only be understood via the quantum-mechanical properties of spin and angular momentum.
If there is sufficient energy exchange between neighbouring dipoles they will interact, and may spontaneously align or anti-align and form magnetic domains, resulting in ferromagnetism (permanent magnets) or antiferromagnetism, respectively. Paramagnetic behavior can also be observed in ferromagnetic materials that are above their Curie temperature, and in antiferromagnets above their Néel temperature. At these temperatures the available thermal energy simply overcomes the interaction energy between the spins.
In general paramagnetic effects are quite small: the magnetic susceptibility is of the order of 10−3 to 10−5 for most paramagnets, but may be as high as 10−1 for synthetic paramagnets such as ferrofluids.
Delocalization
| Material | Magnetic susceptibility (×10−5) |
|---|---|
| Tungsten | 6.8 |
| Cesium | 5.1 |
| Aluminium | 2.2 |
| Lithium | 1.4 |
| Magnesium | 1.2 |
| Sodium | 0.72 |
In many metallic materials the electrons are itinerant, i.e. they travel through the solid more or less as an electron gas. This is the result of very strong interactions (overlap) between the wave functions of neighboring atoms in the extended lattice structure. The wave functions of the valence electrons thus form a band with equal numbers of spins up and down. When exposed to an external field only those electrons close to the Fermi level will respond and a small surplus of one type of spins will result. This effect is a weak form of paramagnetism known as Pauli-paramagnetism. The effect always competes with a diamagnetic response of opposite sign due to all the core electrons of the atoms. Stronger forms of magnetism usually require localized rather than itinerant electrons. However in some cases a bandstructure can result in which there are two delocalized subbands with states of opposite spins that have different energies. If one subband is preferentially filled over the other, one can have itinerant ferromagnetic order. This usually only happens in relatively narrow (d-)bands, which are poorly delocalized.
s and p electrons
Generally, strong delocalization in a solid due to large overlap with neighboring wave functions tends to lead to pairing of spins (quenching) and thus weak magnetism. This is why s- and p-type metals are typically either Pauli-paramagnetic or as in the case of gold even diamagnetic. In the latter case the diamagnetic contribution from the closed shell inner electrons simply wins from the weak paramagnetic term of the almost free electrons.
d and f electrons
Stronger magnetic effects are typically only observed when d- or f-electrons are involved. Particularly the latter are usually strongly localized. Moreover the size of the magnetic moment on a lanthanide atom can be quite large as it can carry up to 7 unpaired electrons. This is one reason why superstrong magnets are typically based on lanthanide elements like neodymium or samarium.
Molecular localization
Of course the above picture is a generalization as it pertains to materials with an extended lattice rather than a molecular structure. Molecular structure can also lead to localization of electrons. Although there are usually energetic reasons why a molecular structure results such that it does not exhibit partly filled orbitals (i.e. unpaired spins), some non-closed shell moieties do occur in nature. Molecular oxygen is a good example. Even in the frozen solid it contains di-radical molecules resulting in paramagnetic behavior. The unpaired spins reside in orbitals derived from oxygen p wave functions, but the overlap is limited to the one neighbor in the O2 molecules. The distances to other oxygen atoms in the lattice remain too large to lead to delocalization and the magnetic moments remain unpaired.
Curie's law
For low levels of magnetization, the magnetization of paramagnets follows Curie's law to good approximation:
where:
- M is the resulting magnetization
- χ is the magnetic susceptibility
- H is the auxiliary magnetic field, measured in amperes/meter
- T is absolute temperature, measured in kelvins
- C is a material-specific Curie constant
This law indicates that the susceptibility χ of paramagnetic materials is inversely proportional to their temperature. Curie's law is valid under the commonly encountered conditions of low magnetization (μBH ≲ kBT), but does not apply in the high-field/low-temperature regime where saturation of magnetization occurs (μBH ≳ kBT) and magnetic dipoles are all aligned with the applied field. When the dipoles are aligned, increasing the external field will not increase the total magnetization since there can be no further alignment.
For a paramagnetic ion with noninteracting magnetic moments with angular momentum J, the Curie constant is related the individual ions' magnetic moments,
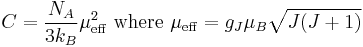 .
.
The parameter μeff is interpreted as the effective magnetic moment per paramagnetic ion. If one uses a classical treatment with molecular magnetic moments represented as discrete magnetic dipoles, μ, a Curie Law expression of the same form will emerge with μ appearing in place of μeff.
-
Click "show" to see a derivation of this law: Curie's Law can be derived by considering a substance with noninteracting magnetic moments with angular momentum J. If orbital contributions to the magnetic moment are negligible (a common case), then in what follows J = S. If we apply a magnetic field along what we choose to call the z-axis, the energy levels of each paramagnetic center will experience Zeeman splitting of its energy levels, each with a z-component labeled by MJ (or just MS for the spin-only magnetic case). Applying semiclassical Boltzmann statistics, the molar magnetization of such a substance is 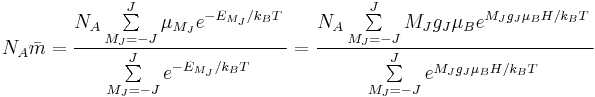 .
.
Where
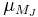 is the z-component of the magnetic moment for each Zeeman level, so
is the z-component of the magnetic moment for each Zeeman level, so 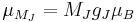 – μB is called the Bohr Magneton and gJ is the Landé g-factor, which reduces to the free-electron g-factor, gS when J = S. (in this treatment, we assume that the x- and y-components of the magnetization, averaged over all molecules, cancel out because the field applied along the z-axis leave them randomly oriented.) The energy of each Zeeman level is
– μB is called the Bohr Magneton and gJ is the Landé g-factor, which reduces to the free-electron g-factor, gS when J = S. (in this treatment, we assume that the x- and y-components of the magnetization, averaged over all molecules, cancel out because the field applied along the z-axis leave them randomly oriented.) The energy of each Zeeman level is 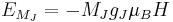 . For temperatures over a few K,
. For temperatures over a few K, 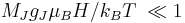 , and we can apply the approximation
, and we can apply the approximation 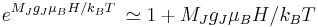 :
: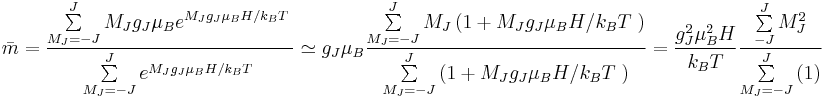 ,
,
which yields:
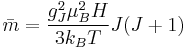 . The molar bulk magnetization is then
. The molar bulk magnetization is then ![M=N_{\text{A}}\bar{m}=\frac{N_{\text{A }}}{3k_{B}T}\left[ g_{J}^{2}J(J%2B1)\mu _{B}^{2}\right]H](/2012-wikipedia_en_all_nopic_01_2012/I/bfeaaac07a723eb6d4068113f99c304a.png) ,
,
and the molar susceptibility is given by
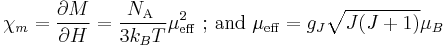 .
.
When orbital angular momentum contributions to the magnetic moment are small, as occurs for most organic radicals or for octahedral transition metal complexes with d3 or high-spin d5 configurations, the effective magnetic moment takes the form (ge = 2.0023... ≈ 2),
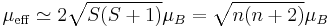 , where n is the number of unpaired electrons. In other transition metal complexes this yields a useful, if somewhat cruder, estimate.
, where n is the number of unpaired electrons. In other transition metal complexes this yields a useful, if somewhat cruder, estimate.
Examples of paramagnets
Materials that are called 'paramagnets' are most often those that exhibit, at least over an appreciable temperature range, magnetic susceptibilities that adhere to the Curie or Curie–Weiss laws. In principle any system that contains atoms, ions or molecules with unpaired spins can be called a paramagnet, but the interactions between them need to be carefully considered.
Systems with minimal interactions
The narrowest definition would be: a system with unpaired spins that do not interact with each other. In this narrowest sense, the only pure paramagnet is a dilute gas of monatomic hydrogen atoms. Each atom has one non-interacting unpaired electron. Of course, the latter could be said about a gas of lithium atoms but these already possess two paired core electrons that produce a diamagnetic response of opposite sign. Strictly speaking Li is a mixed system therefore, although admittedly the diamagnetic component is weak and often neglected. In the case of heavier elements the diamagnetic contribution becomes more important and in the case of metallic gold it dominates the properties. Of course, the element hydrogen is virtually never called 'paramagnetic' because the monatomic gas is stable only at extremely high temperature; H atoms combine to form molecular H2 and in so doing, the magnetic moments are lost (quenched), because the spins pair. Hydrogen is therefore diamagnetic and the same holds true for most elements. Although the electronic configuration of the individual atoms (and ions) of most elements contain unpaired spins, it is not correct to call these elements 'paramagnets' because at ambient temperature quenching is very much the rule rather than the exception. However, the quenching tendency is weakest for f-electrons because f (especially 4f) orbitals are radially contracted and they overlap only weakly with orbitals on adjacent atoms. Consequently, the lanthanide elements with incompletely filled 4f-orbitals are paramagnetic or magnetically ordered.[2]
| Material | μeff/μB |
|---|---|
| [Cr(NH3)6]Br3 | 3.77 |
| K3[Cr(CN)6] | 3.87 |
| K3[MoCl6] | 3.79 |
| K4[V(CN)6] | 3.78 |
| [Mn(NH3)6]Cl2 | 5.92 |
| (NH4)2[Mn(SO4)2]·6H2O | 5.92 |
| NH4[Fe(SO4)2]·12H2O | 5.89 |
Thus, condensed phase paramagnets are only possible if the interactions of the spins that lead either to quenching or to ordering are kept at bay by structural isolation of the magnetic centers. There are two classes of materials for which this holds:
- Molecular materials with a (isolated) paramagnetic center.
- Good examples are coordination complexes of d- or f-metals or proteins with such centers, e.g. myoglobin. In such materials the organic part of the molecule acts as an envelope shielding the spins from their neighbors.
- Small molecules can be stable in radical form, oxygen O2 is a good example. Such systems are quite rare because they tend to be rather reactive.
- Dilute systems.
- Dissolving a paramagnetic species in a diamagnetic lattice at small concentrations, e.g. Nd3+ in CaCl2 will separate the neodymium ions at large enough distances that they do not interact. Such systems are of prime importance for what can be considered the most sensitive method to study paramagnetic systems: EPR.
Systems with interactions
As stated above many materials that contain d- or f-elements do retain unquenched spins. Salts of such elements often show paramagnetic behavior but at low enough temperatures the magnetic moments may order. It is not uncommon to call such materials 'paramagnets', when referring to their paramagnetic behavior above their Curie or Néel-points, particularly if such temperatures are very low or have never been properly measured. Even for iron it is not uncommon to say that iron becomes a paramagnet above its relatively high Curie-point. In that case the Curie-point is seen as a phase transition between a ferromagnet and a 'paramagnet'. The word paramagnet now merely refers to the linear response of the system to an applied field, the temperature dependence of which requires an amended version of Curie's law, known as the Curie–Weiss law:
This amended law includes a term θ that describes the exchange interaction that is present albeit overcome by thermal motion. The sign of θ depends on whether ferro- or antiferromagnetic interactions dominate and it is seldom exactly zero, except in the dilute, isolated cases mentioned above.
Obviously, the paramagnetic Curie–Weiss description above TN or TC is a rather different interpretation of the word 'paramagnet' as it does not imply the absence of interactions, but rather that the magnetic structure is random in the absence of an external field at these sufficiently high temperatures. Even if θ is close to zero this does not mean that there are no interactions, just that the aligning ferro- and the anti-aligning antiferromagnetic ones cancel. An additional complication is that the interactions are often different in different directions of the crystalline lattice (anisotropy), leading to complicated magnetic structures once ordered.
Randomness of the structure also applies to the many metals that show a net paramagnetic response over a broad temperature range. They do not follow a Curie type law as function of temperature however, often they are more or less temperature independent. This type of behavior is of an itinerant nature and better called Pauli-paramagnetism, but it is not unusual to see e.g. the metal aluminium called a 'paramagnet', even though interactions are strong enough to give this element very good electrical conductivity.
Superparamagnets
Some materials show induced magnetic behavior that follows a Curie type law but with exceptionally large values for the Curie constants. These materials are known as superparamagnets. They are characterized by a strong ferromagnetic or ferrimagnetic type of coupling into domains of a limited size that behave independently from one another. The bulk properties of such a system resembles that of a paramagnet, but on a microscopic level they are ordered. The materials do show an ordering temperature above which the behavior reverts to ordinary paramagnetism (with interaction). Ferrofluids are a good example, but the phenomenon can also occur inside solids, e.g., when dilute paramagnetic centers are introduced in a strong itinerant medium of ferromagnetic coupling such as when Fe is substituted in TlCu2Se2 or the alloy AuFe. Such systems contain ferromagnetically coupled clusters that freeze out at lower temperatures. They are also called mictomagnets.
See also
References
- Charles Kittel, Introduction to Solid State Physics (Wiley: New York, 1996).
- Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
- John David Jackson, Classical Electrodynamics (Wiley: New York, 1999).
- ^ Nave, Carl L. "Magnetic Properties of Solids". HyperPhysics. http://hyperphysics.phy-astr.gsu.edu/Hbase/tables/magprop.html. Retrieved 2008-11-09.
- ^ J. Jensen and A. R. MacKintosh, "Rare Earth Magnetism". http://www2.nbi.ku.dk/page40667.htm. Retrieved 2009-07-12., (Clarendon Press, Oxford: 1991).
- ^ A. F. Orchard, Magnetochemistry, (Oxford University Press: 2003).
External links
- Electromagnetism – a chapter from an online textbook
http://www.ndt-ed.org/EducationResources/CommunityCollege/MagParticle/Physics/MagneticMatls.htm
|
|||||